递归

一个函数直接或间接地调用自身，视为直接或间接递归

递归通常需要有边界条件、前进段、返回段，边界条件不满足时，递归前进，满足时，递归返回，递归一般用于解决三类问题：

• 数据的定义是按递归定义的（斐波那契数列，n 的阶乘）
• 问题解法按递归实现（回溯）
• 数据的结构形式按递归定义的（二叉树遍历，图的搜索）

缺点：

• 相对于常用的算法（如普通循环）等，运行效率低，因此尽量避免使用
• 除非没有更好的算法或者某种特定情况，递归更为适合的时候
• 在递归调用的过程中，系统为每一层的返回点、局部量等开辟了栈来存储
• 因此递归次数过多容易造成栈溢出

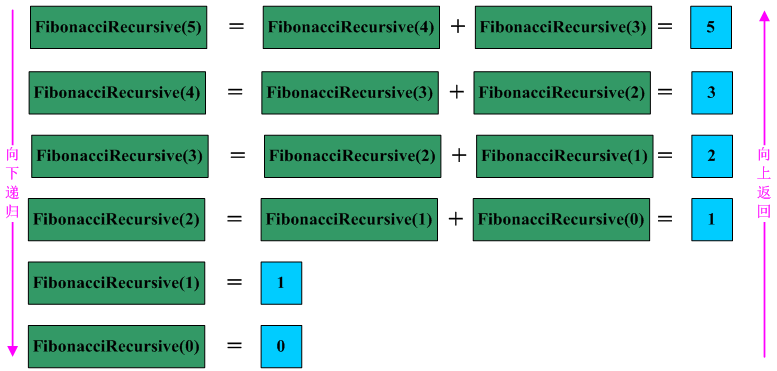
普通递归

function fibonacci(n) {
    if (n < 2) {
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

尾递归

尾递归就是从最后开始计算，每递归一次就算出相应的结果，函数调用出现在函数的尾部，因为是尾部，所以没有必要去保存任何局部变量，直接让被调用的函数返回时越过调用者

尾递归就是把当前运算结果（或路径）放在参数里传给下层函数，深层函数所面对的是越来越复杂的问题（而不是越来越简单的问题），因为参数里带有前面若干步的运算结果

尾递归无需向上返回，但是需要引入额外的空间来保持当前的结果

function fibonacci(n, ret1, ret2) {
    if (n == 0) {
        return ret1;
    }
    return fibonacci2(n - 1, ret2, ret1 + ret2);
}